Counting on the Concrete to Understand Math

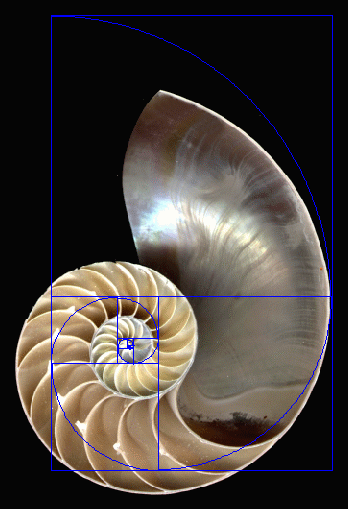
By Margaret Zheng

If you read my previous article on the need to change our perspective on mathematical learning (and if you haven't, I suggest doing so before continuing), it may have struck you that I did not provide any concrete suggestions for improving how we learn mathematics.  Rather, I painted rhetorically with a broad brush and sparkly colors, talking of magic and educational ideals and pulling theory out of the psychological hat.  I could say, hey, I'm a child of the abstract.  And isn't that what math is - abstraction?  

Well, yes.  Just as a rainforest is its canopy.  

The thing is, what mathematics publishes itself as -- numbers and symbols and abstract manipulations -- is really only the visible upper surface of a complex, creative, concrete process.  Physical, usually visual, models become your tools to branching into clearer thought.  Once mathematicians have grasped one concept using pictures or 3-D models, they refer endlessly to the concrete tools to extend their concepts and construct more mathematics, so much so that mathematician James Gleick remarked, "It's masochism for a mathematician to do without pictures" (link).  Thus came such wonders as graphs, number lines, modeling clay, crayons, markers...and fingers.  

Does the last one surprise, or even disgust, you?  Perhaps you were told that only little kids just beginning to learn their numbers use fingers in math.  Perhaps you were directed by your parent or teacher (or Kumon instructor) to stop counting with fingers and get on to the "real" math of memorizing your addition and subtraction.  

Yet brain research has shown that even beyond basic counting, mathematics - and mathematicians themselves, mental calculators or not - depend on those fingers.  When calculating without finger-counting, the area of our brain that "sees" fingers lights up with activity, as if representations of fingers were still used for arithmetic.  In one study, six-year-olds who were better able to identify without sight which finger was touched by an investigator were more likely to see future mathematical success than those who simply scored high on cognitive tests.  Even finger-savvy college students have been found to have higher calculative skill, and those who improved finger awareness also improved arithmetically (link).

It appears that if you brushed up your piano skills or practiced your typing, you might kick-start your brain into thinking more comfortably as a mathematician.  In fact, Jo Boaler, the educational researcher I mentioned in my previous article, suggests finger coordination activities for classroom use, which can be found on www.youcubed.org/visual-math .  But just as important as finger-representation in the mathematician's brain are visual and spatial processing, which along with many other areas of the brain, "light up" when we reason mathematically.  
 
Clearly, there is no one "math skill" that American culture could identify its imagined "math people" to be born with.  By creating visual tools like diagrams or digital models or even "acting out" mathematics with friends (for according to mathematician Keith Devlin, mathematical ability may evolutionarily be a mere extension of the social calculations humans make), we can make even the seemingly most difficult mathematics intuitive.  
 
The usage of concrete tools to aid understanding of mathematics even applies to the Common Core Standards for Mathematical Practice, which mention graphs, diagrams, and technology under "Make sense of problems and persevere in solving them" and "Use appropriate tools strategically," giving additional motive for us to explore these representations of mathematics in class.  All of us, even those historically troubled with math, have the potential to grow our ability to manage the abstract by bridging from the concrete.  

To give an example of gaining mathematical intuition through modeling, I say that instead of pressuring ourselves to quit finger-counting and start mindlessly memorizing, we should explore the idea of adding 6 + 8 by playing with blocks or dots on a page and finding that 4 + (2 + 8) = 4 + 10 and other simpler calculations give the same result.  The method generalizes to large, "scary" sums like 385 + 218 (that is, (385 + 15) + 203 = 400 + 203) and also to algebra (including "completing the square" problems like x2 + 4x - 1 = (x 2 + 4x + 4) - 5, which can also be done with literal square diagrams).  Might I say that in geometry you also can find areas by moving pieces around, and that calculus is a mere extension?  Everything is connected in mathematics, conceptually and neurologically.  Learning, at its most basic, is association - that is, making connections between what one knows already and what one must now grasp.  

So I have now provided some concrete suggestions for mathematical learning to bridge the gap from the persuasive poetry of my previous article.  Now that summer is to begin, you (students and adults) must assign yourself a mission.  Not "homework."  A mission.  You are to be motivated to engage with math.  
 
Short of poring over textbooks while your family and friends enjoy the beach, go pick up seashells in the sand and marvel at the frequent appearance of the golden ratio, which also appears in the Parthenon and in Renaissance art.  
 
Try the Rubik’s cube (I have yet to do so myself!), play math-related computer games like Dragon Box or even the Creative Mode of Minecraft, learn basic computer programming on Khan Academy, solve mathematical and logical puzzles, read books like The Number Devil (a children’s fantasy fit for all), and exercise your finger coordination on a musical instrument.  Seek out math in your everyday life, or even better, try to avoid it completely.  I bet you can’t!  Mathematics is not a chore of school, rather a never-ending game of the mind, infused in all we do.  
 
The end of the school year calls for reflection on how we have contributed to the learning process and how we can learn better.  Even senior students share this obligation; as a senior friend said to me, do you stop caring about something just because you are leaving it?  We reflect upon ourselves, as individuals and as a cooperative community.  Students, when you next see your math teachers, thank them for helping you grow as a mathematician, and tell them in person or in writing what you would like them to do more in class.  That could be something the teachers already do and should continue or something you want them to start.  Teachers, thank in turn your students for their insights and their energy, and tell them what you want them to do more for their continued education and growth.  
 
Working together, we grasp the abstract ideals we dream of and unite them with the concrete ground.  

---